Das Perzeptron wird optimiert
Michael Seibel • Gradientenabstieg, Faltungsnetze und andere..., Lokale Empfangsfelder, Filter, Pooling-Schichten (Last Update: 01.07.2020)
Der Gradientenabstieg
Der Gradientenabstieg ist ein generalisierbarer Algorithmus zur Optimierung, der in vielen Verfahren des maschinellen Lernens zur Anwendung kommt, jedoch ganz besonders als sogenannte Backpropagation im Deep Learning den Erfolg der künstlichen neuronalen Netze erst möglich machen konnte. Die Aufgabe des Gradientenabstiegs besteht darin, anhand eines iterativen Prozesses einen Satz von Parametern zu verfeinern, wobei partielle Differentialgleichungen verwendet werden.
Das Prinzip des Gradientenabstiegs lässt sich veranschaulichen: Angenommen, man stünde im Gebirge im dichten Nebel. Der Weg ins Tal ist vom Nebel verdeckt. Wohin sollte man laufen? Man kann das Ziel zwar nicht sehen, kann sich jedoch so herantasten, dass man den Gradienten (den Unterschied der Höhen beider Füße) berechnet. Damit kennt man die Steigung des Bodens und kann entgegen dieser Steigung seinen Weg fortsetzen.
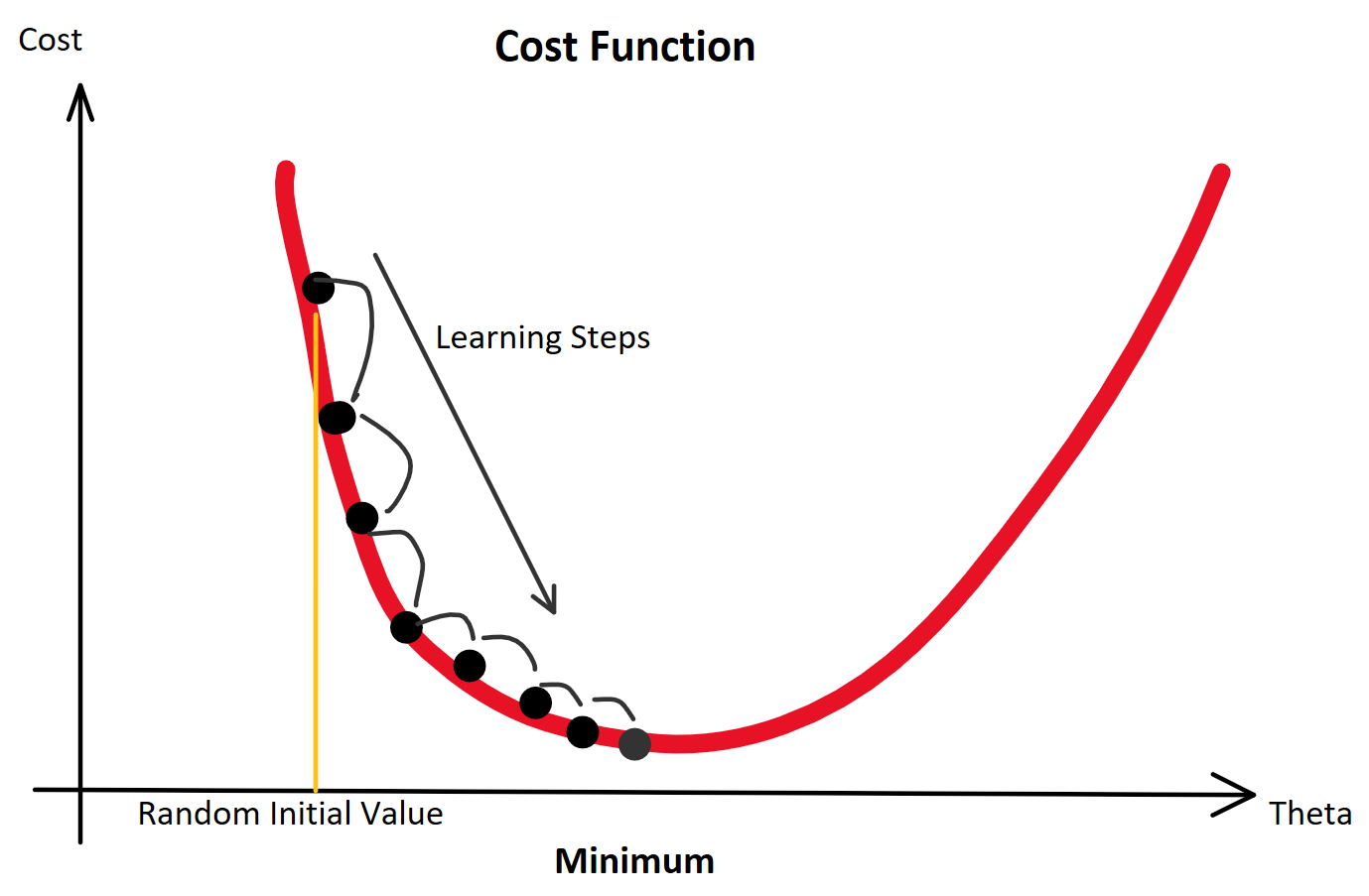
Konkret funktioniert der Gradientenabstieg so: Man startet bei einem zufälligen Theta (Random Initialization). Man berechnet die Ausgabe (Forwardpropogation) und vergleicht sie über eine Verlustfunktion mit dem tatsächlich korrekten Wert. Auf Grund der zufälligen Initialisierung beginnt man mit einem Ergebnis, das wahrscheinlich falsch ist und somit mit einem Verlust. Für die Verlustfunktion berechnen wir den Gradienten für gegebene Eingabewerte. Voraussetzung dafür ist, dass die Funktion ableitbar ist. Wir bewegen uns entgegen des Gradienten in Richtung des Minimums der Verlustfunktion. Ist dieses Minimum (fast) gefunden, spricht man davon, dass der Lernalgorithmus konvergiert.
Befinden wir uns nur zwischen zwei Bergen, finden wir das Tal mit Sicherheit über den Gradienten. Befinden wir uns jedoch in einem Gebirge mit vielen Tälern, gilt es, das richtige Tal zu finden, das am tiefsten liegt. Bei der Optimierung der Gewichtungen von künstlichen neuronalen Netzen gilt es, die besten Gewichtungen zu finden, die zu den geringsten Ausgaben der Verlustfunktion führen. Man sucht also das globale Minimum unter den möglicherweise Tausenden lokalen Minima einer möglicherweise vieltausend-dimensionalen Funktion. Das bedarf enormer Rechenleistung.
Zur Bestimmung der Größe jedes Schritts während des Gradientenabstiegsprozesses wird die sog. Lernrate verwendet. Eine geringe Lernrate kann zur Verlangsamung des Gradientenabstiegsprozesses führen. Eine hohe Lernrate kann dagegen zum Überschreiten des Minimums und zum Scheitern des Konvergierens oder sogar zum Divergieren führen. Wenn die Lernrate festgelegt ist, kann der Gradientenabstieg zu einem lokalen Minimum konvergieren. Nähert man sich einem lokalen Minimum, so werden automatisch kleinere Schritte gemacht.
Nach
der Recheneffizienz unterscheidet man mehrere Hauptarten des
Gradientenabstiegs, die in KI-Algorithmen verwendet werden. Da ein
Datensatz aus Millionen oder sogar Milliarden von Datenpunkten
bestehen kann, kann die Berechnung des Gradienten über den
gesamten Datensatz rechnerisch extrem aufwändig sein. Das ist
einer der Gründe, warum die Frage entscheidend ist, auf welche
Weise neuronale Netze physikalisch-materiell realisiert sind.
Außerdem ist es entsprechend unwahrscheinlich, dass das gefundene lokale Optimum auch das globale Optimum ist.
Ein hoher Anteil der Forschungsarbeit an neuronalen Netzwerken dient der Verbesserung der Backpropagation, des Gradientenabstiegs.
Faltungsnetze und andere...
Bis hierhin wurde ein Netzwerk vorgestellt, in dem benachbarte Netzwerkschichten vollständig miteinander verbunden sind. Jedes Neuron im Netzwerk ist mit jedem Neuron in benachbarten Schichten verbunden. Für die Bilderkennung sind solche Netze insofern nicht optimal, als sie die räumliche Struktur von Bildern nicht berücksichtigen. Im Gegenteil wird die Beziehung weit voneinander entfernter Pixel genau so behandelt wie die von eng beieinanderliegenden Pixeln. Räumliche Nachbarschaftsbeziehungen bleiben unberücksichtigt. Dennoch ist in der oben schon beschrieben Art und Weise immerhin 98% Erkennungsgenauigkeit erreichbar.
Bei einem weiterführenden Typ von Netzwerken für die Bild- und der Spracherkennung wird eine andere Architektur eingesetzt, die sog. deep convolutional networks oder Faltungsnetzwerke.
Mit Hilfe einiger weiterer Techniken (dazu gleich mehr) wie Convolutions/Faltungen, Pooling, die Verwendung von GPUs, der algorithmischen Erweiterung der Trainingsdaten, um weitaus mehr Training mit künstlichen Trainingsdaten durchführen zu können und so Überanpassung zu reduzieren, der Verwendung der Dropouts Technik (ebenfalls, um Überanpassung zu reduzieren) und die Verwendung ganzer Ensembles von Netzwerken (zu all dem gleich etwas mehr), erreicht das System nahezu menschliche Leistung beim Erkennen handgeschriebener Ziffern. Von den 10.000 MNIST-Testbildern klassifiziert es dann 9.967 korrekt.
Die genannten erweiterten Techniken im einzelnen:
Faltungsnetzwerke verwenden eine spezielle Architektur, die besonders gut zur Klassifizierung von Bildern geeignet ist. Durch die Verwendung dieser Architektur können Faltungsnetzwerke schneller trainiert werden. Dies hilft wiederum dabei, tiefe, vielschichtige Netzwerke zu trainieren, die sich sehr gut für die Klassifizierung von Bildern eignen. Heutzutage werden in den meisten neuronalen Netzen tiefe Faltungsnetzwerke oder eine nahe Variante zur Bilderkennung verwendet.
Faltungs-Neuronale Netze verwenden dabei drei Grundideen: lokale Empfangsfelder, gemeinsame Gewichte und Pooling.
Lokale Empfangsfelder: In den zuvor gezeigten vollständig verbundenen Schichten wurden die Eingaben als vertikale Linie von Neuronen dargestellt. In einem Faltungsnetz hilft es, anstelle dessen die Eingaben als quadratische Felder von 28 × 28 Pixel vorzustellen, deren Werte ebenfalls den jeweiligen Pixelintensitäten entsprechen.

Jetzt wird allerdings nicht wie bisher jedes Eingangspixel mit allen Neuronen des übergeordneten Hidden Layer verbunden. Stattdessen werden Verbindungen nur in kleinen, lokalisierten Bereichen des Eingabebildes hergestellt. Jedes Neuron in der ersten verborgenen Schicht ist lediglich mit einem kleinen Bereich der Eingangsneuronen verbunden, beispielsweise mit 5 × 5 = 25 Neuronen. Für ein bestimmtes verstecktes Neuron könnten die Verbindungen also so aussehen:
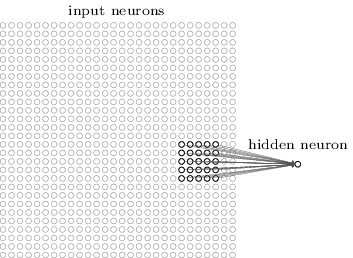
Dieser Bereich im Eingabebild wird als lokales Empfangsfeld für das verborgene Neuron bezeichnet. Es ist ein kleines Fenster auf den Eingabepixeln. Jede der so hergestellten Verbindung erhält ein Gewicht, das bei den folgenden Iterationen trainiert wird. Und das versteckte Neuron lernt auch einen Bias. Auf diese Weise lernt das versteckte Neuron, sein bestimmtes lokales Empfangsfeld zu analysieren.
Man startet links oben und verschiebt dann das lokale Empfangsfeld schrittweise nach rechts über das gesamte Eingabebild und dann zeilenweise nach unten und erhält so die weiteren Eingaben für den ersten Hidden Layer. Für jedes lokale Empfangsfeld gibt es in der ersten verborgenen Schicht ein anderes verstecktes Neuron. Um dies konkret zu veranschaulichen, beginnt man mit einem lokalen Empfangsfeld in der oberen linken Ecke:

Dann schiebt man das lokale Empfangsfeld um ein Pixel nach rechts (d. H. um ein Neuron), um eine Verbindung zu einem zweiten versteckten Neuron herzustellen:

In diesem Beispiel wird das lokale Empfangsfeld jeweils um ein Pixel verschoben. Bei größeren Bildern können auch größere Schrittlänge zweckmäßig sein.
Geteilte Gewichte und Bias': Jedes versteckte Neuron hat eine Bias und 5 × 5 Gewichte, die mit seinem lokalen Empfangsfeld verbunden sind. Für jedes der versteckten 24 × 24-Neuronen sollen jetzt jedoch die gleichen Gewichte und Bias' verwendet werden. Damit wird aus einer solchen Karte an Werten das, was man in der Bildverarbeitung ein Filter nennen würde.
Dies bedeutet, dass alle Neuronen in der ersten verborgenen Schicht genau dasselbe Merkmal erkennen. Es kann beispielsweise eine Kante im Bild oder eine andere Form sein, nur an verschiedenen Stellen im Eingabebild. Um zu verstehen, warum das sinnvoll ist, nehmen wir an, dass die Gewichte und die Bias' so gewählt sind, dass das verborgene Neuron beispielsweise eine vertikale Kante in einem bestimmten lokalen Empfangsfeld erkennen kann. Diese Fähigkeit ist wahrscheinlich auch an anderen Stellen im Bild nützlich. Daher ist es nützlich, überall im Bild denselben Feature-Detektor anzuwenden. Bewegt man beispielsweise das Bild einer Katze ein wenig, bleibt es immer noch das Bild einer Katze, obwohl jedes einzelne Pixel einen anderen Grauwert bekommen hat.
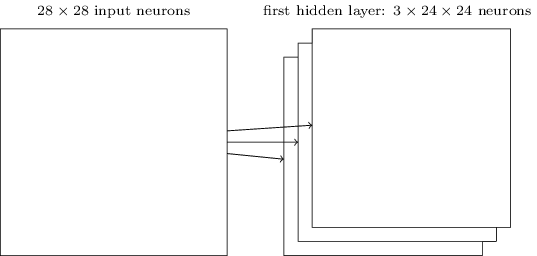
Für
die Bilderkennung benötigt man mehr als eine Feature-Map. Eine
vollständige Faltungsschicht besteht also aus mehreren
verschiedenen Feature-Maps:
Im Beispiel sind es 3 Feature-Maps. Jede Feature-Map wird durch einen Satz von 5 × 5 gemeinsamen Gewichten und eine einzelne gemeinsame Vorspannung definiert. Das Ergebnis ist, dass das Netzwerk drei verschiedene Arten von Merkmalen erkennen kann, wobei jedes Merkmal über das gesamte Bild hinweg erkennbar ist. Hier im Beispiel werden der Einfachheit halber nur 3 Feature-Maps gezeigt. In der Praxis können es sehr viel mehr sein.
Ein kurzer Blick auf einige der gelernten Funktionen. Die abgebildeten Funktionskarten stammen aus dem endgültigen Faltungsnetzwerk, das trainiert wurde.

Die 20 Bilder entsprechen 20 verschiedenen Feature-Maps oder Filtern. Jede Karte wird als 5 × 5-Blockbild dargestellt, das 5 × 5 Gewichte im lokalen Empfangsfeld entspricht. Weißere Blöcke bedeuten ein kleineres (normalerweise negativeres) Gewicht, sodass die Feature-Map weniger auf entsprechende Eingabepixel reagiert. Dunkle Blöcke bedeuten ein größeres Gewicht, sodass die Feature-Map stärker auf die entsprechenden Eingabepixel reagiert. Grob gesagt zeigen die obigen Bilder die Art der Merkmale, auf die die Faltungsschicht reagiert.
Was lässt sich aus diesen Feature-Maps schließen? Es ist klar, dass es hier eine räumliche Struktur gibt: Viele der Merkmale haben klare Unterbereiche von hell und dunkel. Das zeigt, dass das Netzwerk wirklich Dinge lernt, die mit der räumlichen Struktur zusammenhängen. Darüber hinaus ist es jedoch ziemlich unklar, was diese Feature-Detektoren eigentlich lernen. Tatsächlich wird jetzt viel daran gearbeitet, die von Faltungsnetzwerken erlernten Funktionen besser zu verstehen.1
(Und in der Tat erkennen neuronale Netze unter anderem auch Muster, die von menschlichen Beobachtern weder entdeckt worden wären, noch für signifikant gehalten werden, wenn sie sie vorgelegt bekommen. Wir kommen unten noch darauf zurück.)
Das Teilen von Gewichten und Bias' reduziert die Anzahl der in einem Faltungsnetzwerk beteiligten Parameter erheblich. Für jede Feature-Map benötigen wir 25 = 5 × 5 gemeinsame Gewichte plus eine einzige gemeinsame Bias. Für jede Feature-Map sind also 26 Parameter erforderlich. Wenn wir 20 Feature-Maps haben, sind das insgesamt 20 × 26 = 520 Parameter, die die Faltungsschicht definieren. Zum Vergleich hätten man bei einer vollständig verbundenen ersten Schicht mit 784 = 28 × 28 Eingangsneuronen und relativ bescheidenen 30 versteckten Neuronen, wie oben verwendet insgesamt 784 × 30 Gewichte plus 30 zusätzliche Bias mit insgesamt 23.550 Parametern. Mit anderen Worten hätte die vollständig verbundene Schicht mehr als 40 mal so viele Parameter wie die Faltungsschicht. Das lässt die Vermutung zu, dass das Faltungsnetzwerk mit erheblich geringerem Trainingsaufwand auskommt.
Pooling-Schichten: Zusätzlich zu den gerade beschriebenen Faltungsschichten enthalten Faltungs-Neuronale Netze auch Pooling-Schichten. Pooling-Schichten werden normalerweise unmittelbar nach Faltungsschichten verwendet. Die Pooling-Schichten kondensieren die Informationen der Faltungsschicht. Zum Beispiel kann jedes Neuron der Pooling-Schicht einen Bereich von beispielsweise 2 × 2 Neuronen der vorherigen Schicht zusammenfassen. Beim Max-Pooling übernimmt ein Pooling-Neuron einfach die maximale Aktivierung von 2 × 2 ihr zugeordneten Neuronen aus dem Eingabebereich:

Die Faltungsschicht umfasst normalerweise mehr als einen einzelnen Filter. Max-Pooling wird für jede Feature-Map separat angewandt. Wenn es also drei Feature-Maps gäbe, würden die kombinierten Faltungs- und Max-Pooling-Ebenen folgendermaßen aussehen:
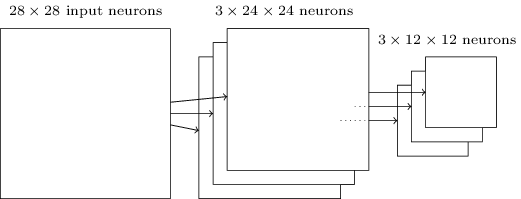
Max-Pooling funktioniert da besonders gut, wo es nicht um die genaue Position von Merkmalen, sondern um ihr Vorhandensein und um die relative Position zu anderen Merkmalen geht. Außerdem reduziert sie nochmals erheblich die Anzahl von Parametern, die trainiert werden müssen.
Max-Pooling ist natürlich auch wieder nicht die einzige Pooling-Technik.
Alle diese Ideen lassen sich zusammenfügen, um ein vollständiges neuronales Faltungsnetzwerk zu bilden. Es ähnelt der Architektur, die gerade betrachtet wurde, hat jedoch eine zusätzliche Schicht von 10 Ausgangsneuronen, entsprechend der 10 möglichen Werte für MNIST-Ziffern.
Das Netzwerk beginnt mit 28 × 28 Eingangsneuronen, mit denen die Pixelintensitäten für das MNIST-Bild codiert werden. Darauf folgt eine Faltungsschicht unter Verwendung eines lokalen 5 × 5-Empfangsfeldes und 3 Merkmalskarten. Das Ergebnis ist eine Schicht von 3 × 24 × 24 Neuronen mit versteckten Merkmalen. Der nächste Schritt ist eine Max-Pooling-Ebene, die auf 2 × 2 Regionen über jede der 3 Feature-Maps angewendet wird. Deren Ergebnis ist eine Schicht von 3 × 12 × 12 Neuronen mit versteckten Merkmalen. Die letzte Schicht der Verbindungen im Netzwerk ist eine vollständig verbundene Schicht. Das heißt, diese Schicht verbindet jedes Neuron von der Max-Pool-Schicht mit jedem der 10 Ausgangsneuronen. Trainiert wird auch hier wieder mit stochastischem Gradientenabstieg und Backpropagation.2
So weit, so gut. Hier die 33 Bilder, die falsch klassifiziert wurden. (Jeweils oben rechts der korrekte Wert, unten rechts der Schätzwert des Netzwerks)

Viele davon sind auch für einen Menschen kaum zu klassifizieren. Das Ergebnis kann sich also sehen lassen.
Anmerkungen:
1 Zur Vertiefung: Visualizing and Understanding Convolutional Networks von Matthew Zeiler und Rob Fergus (2013). (https://arxiv.org/abs/1311.2901)
2 Rodrigo Benenson hat eine informative Übersichtsseite zusammengestellt, die die Fortschritte im Laufe der Jahre zeigt und Links zu Artikeln enthält. http://rodrigob.github.io/are_we_there_yet/build/classification_datasets_results.html
zurück ...
weiter ...
Ihr Kommentar
Falls Sie Stellung nehmen, etwas ergänzen oder korrigieren möchten, können sie das hier gerne tun. Wir freuen uns über Ihre Nachricht.

