Also rein ins Geschehen! In Folgendem möchte ich eine konkrete Technik, die automatische Erkennung von Handschriften auf ihren erkenntnistheoretischen Gehalt hin auslegen, durchaus nicht grundsätzlich anders, als wenn ich einen Text Shakespeares interpretieren würde. Ein Stück klassische Bildung und eine gewisse Kompetenz zur Literaturinterpretation traut man uns ja zu. Unter einer philosophischen Interpretation von technischen Algorithmen kann man sich dagegen meist nur wenig vorstellen, es sei denn ein äußerliches Lamentieren nach dem Motto, den Sonntag der Philosophie, aber die ganze Woche der Technik. Wir lesen also den technischen Diskurs nicht als Lieferanten von Techniken, sondern als Lieferanten reflektierbarer Gedanken und Texte.

Die Frage an unser Musterbeispiel ist: wie erkennt ein neuronales Netz handgeschriebene Ziffern. An Erinnerungen, an Ahnungen, an Identitäten oder an irgendwelchen Zufälligkeiten? Es ist das Vorzeigemodell, mit dem Google als einer der Hauptentwickler von Artificial Intelligence (AI) Interessierten die Arbeitsweise von deep learning mittels neuronaler Netze näherbringt.

Die leitende Frage der Entwickler war die folgende: Was ist nötig, um ein neuronales Netz zu erzeugen, das handgeschriebene Ziffern korrekt lesen kann?

Ein künstliches neuronales Netz besteht aus sog. Perzeptronen oder Neuronen. Perzeptronen wurden in den 1950er und 1960er Jahren von Frank Rosenblatt entwickelt, inspiriert von früheren Arbeiten von Warren McCulloch und Walter Pitts.

Ein Perzeptron ist zunächst einmal ein Gedankending, ein theoretisches Konzept. Ein Perzeptron benötigt ein oder mehrere Binäreingänge, x₁, x₂,… und erzeugt einen einzelnen Binärausgang:

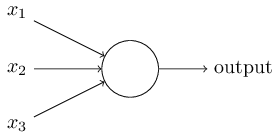
Rosenblatt schlug eine einfache Regel zur Berechnung der Ausgabe vor. Er führte Gewichte w₁, w₂, ...w_j ein, reelle Zahlen, die die Wichtigkeit der jeweiligen Eingaben für die Ausgabe ausdrücken. Die Ausgabe des Neurons wird dadurch bestimmt, ob die gewichtete Summe ∑_jw_jx_j kleiner oder größer als ein Schwellenwert ist. Genau wie die Gewichte ist der Schwellenwert eine reelle Zahl, die ein Parameter des Neurons ist.

(1)

Ausgabe =
0 if ∑_jw_jx_j≤ Schwelle
1 if ∑_jw_jx_j> Schwelle

Das Perzeptron ist also eigentlich ein mathematisch-logisches Modell. Die Idee des Perzeptrons hat aber den zweiten Hauptaspekt, dass diese mathematische Modell irgendwie physikalisch-technisch realisiert werden soll. Ein Perzeptron wird so zu einem elementaren technischen Gerät, das abhängig von einem Schwellwert Entscheidungen trifft.

Beispiel: Am Wochenende läuft eine Party. Ob Sie hingehen oder nicht machen Sie davon abhängig, ob (x₁) jemand hinkommt, den Sie schon lange einmal kennenlernen wollten, ob (x₂) ihre Freunde auch da sind, ob (x₃) gute Musik zu erwarten ist, ob man (x₄) tanzen kann oder nicht, (x₅) wann Sie am nächsten Tag arbeiten müssen, ob (x₆) öffentliche Verkehrsmittel in der Nähe sind und ob es (x₇) regnet oder nicht.

Das ließe sich z.B. mit 7 Inputneuronen und 1 Outputneuron darstellen. Dabei steht jedes Inputneuron für einen der Gründe (x₁ … x₇), die jeweils gewichtet werden müssen (w₁ … w₇), und das Outputneuron natürlich für die Antwort auf die Frage, ob man an der Party teilnimmt.

Die Frage, ob (x₁) jemand hinkommt, den Sie schon lange einmal kennenlernen wollten, ist mit ja=1 oder nein=0 beantwortbar oder mit einer Wahrscheinlichkeit dazwischen. Die Frage ist allerdings, für wie wichtig man es hält, diese Person zu treffen. Aus diese Weise sind die Fragen durchzugehen, zu beantworten und zu gewichten. Das Ergebnis könnte z.B. sein:

(x₁) der interessante Mensch, den Sie immer schon kennenlernen wollten, kommt vielleicht, und das wäre sehr wichtig, (x₂) ihre Freunde sind auch da, auch das ist ziemlich wichtig, (x₃) gute Musik ist eher nicht zu erwarten, was ihnen aber egal ist, (x₄) tanzen kann man wahrscheinlich nicht, (x₅) am nächsten Tag müssen Sie leider früh raus, was gar nicht gut ist (x₆), öffentliche Verkehrsmittel sind leider nicht in der Nähe und (x₇) als sie losgehen wollen stellen Sie fest, dass es nicht regnet. Das könnte man etwa folgendermaßen ausdrücken:

∑_jw_jx_j = (w₁)*(x₁) + … + (w₇)*(x₇)
= Beispiel: 5*0,5 + 3*1 + 2*0,5 + 1*0 + 4*0 + 0*0 + 3*1 = 9,5

9,5 Punkte für die Party. Geht man jetzt hin oder nicht? Es ist ja einiges nicht so toll, schlechte Musik, am nächsten Tag früh zur Arbeit … aber andererseits ... Was fehlt, ist ein Schwellwert. Setzt man ihn in diesem Fall höher als 9,5 , dann hat man sich gegen die Party entschieden, sonst geht man hin.

Durch Variation der Gewichte und der Schwelle können wir also ganz verschiedene Modelle der Entscheidungsfindung erhalten und damit auch alle überhaupt denkbaren Ergebnisse.

Sowohl die einzelnen Gewichte wie der Schwellwert sind willkürliche Setzungen. Die X-Werte dagegen, die als Inputs dienen, sind Schätzungen und Messungen (im Beispiel: es regnet/es regnet nicht). … erkenntnistheoretisch wohl eine interessante Mischung!

Dieses einschichtige Modell bildet menschliche Entscheidungsfindung natürlich schon allein deshalb nicht ausreichend ab, weil es nicht angeben kann, wie man an die entsprechenden Gewichte und Schwellwerte kommt. Aber man sieht zumindest, dass sich grundsätzlich eine ganze Reihe von Gründen für eine Entscheidung berücksichtigen lassen und man kann sich vorstellen, dass man recht komplexe Entscheidungswege abbilden kann, wenn man mit mehrschichtigen Netzen arbeitet, bei denen die Inputschicht ihr Ergebnis nicht direkt in die Outputschicht einspeist, sondern in eine Zwischenschicht, in den sog. hidden layer, der an die Entscheidungen der Eingabeschicht weiter differenzierende Kriterien anlegt und dann seine eigenen Entscheidungen an die Outputschicht oder an eine weitere Zwischenschicht weitergibt.

Formel (1) lässt sich umformen in:

(2)

Ausgabe =
0 if w_*x + b ≤ 0
1 if w_*x + b > 0

Der Term b steht dabei für Bias. Das ist der Schwellwert, der zuvor auf der anderen Seite der Ungleichung stand. Der Bias ist ein Maß dafür, wie einfach es ist, das Perzeptron dazu zu bringen, eine 1 auszugeben.

Kommen wir hier noch einmal auf den eigentlichen Gedanken zu sprechen, der bis hierhin zu erkennen ist: Wir haben ein zunächst einfaches mathematisch-logisches Modell, eine Ungleichung, also Quantitäten, Identität und Differenz. Auf welcher physikalisch-materiellen Basis das Modell realisiert werden soll, ist noch völlig unbestimmt. Von Ähnlichkeit ist bis hierhin überhaupt noch nicht die Rede, wohl aber von Entscheidungen.

Allerdings ist bis hierhin auch alles, was Perzeptronen zu Abbildungsmöglichkeiten von Entscheidungen macht, dem Modell völlig äußerlich. Es gibt nur leere Formen, die Input aufnehmen können, leere Formen für Gewichtungen und eine andere leere Form, die den Bias aufnimmt und es gibt eine allerdings strenge Rechenregel, die angibt, wie mit möglichen Inhalten zu verfahren wäre und die eben auch die Form bestimmt, die mögliche Inhalte haben müssen. Es müssen arithmetische Größen sein.

Die Befüllung der leeren Form mit dem Gegenstand der Entscheidung hätte ein Mensch vorzunehmen, jemand, der sagt, was überhaupt zu entscheiden ist, der es quantifiziert und die Gewichtungen festlegt. Als menschliches Denken ist ein solches Ensemble natürlich real. Dort kommt in der Tat alles nötige zusammen, all die Elemente, die wir gerade benannt haben, z.B. bei der Abwägung, auf eine Party zu gehen. Arithmetische Rechenleistung würde man dabei allerdings nur für den Kauf von Rotweinflasche oder Blumenstraus brauchen, den man gegebenenfalls mitbringen möchte.

Teile des Ensembles, nämlich der Teil, der als Perzepton gedacht wird, lassen sich allerdings auf ganz unterschiedliche Weise auch technisch realisieren z.B. in Form einer mechanischen Rechenmaschine, also ohne jede Computertechnik und ohne Digitalisierung. Vermutlich wäre schon die 1673 von Gottfried Wilhelm Leibniz entwickelte Staffelwalzen-Rechenmaschine geeignet gewesen.

Zu den ersten Rechenmaschinen aus der ersten Hälfte des 17. Jahrhunderts von Schickard und Blaise Pascal ist zu lesen:

„Beide Maschinentypen haben ein gemeinsames Problem. Sie eignen sich nicht für den alltäglichen Einsatz als Rechenmaschinen. Sie enthalten wichtige Funktionsprinzipien, nicht aber Vorrichtungen, die das tägliche sichere Arbeiten ermöglichen.
So fehlt der Maschine von Wilhelm Schickard die Möglichkeit, Energie für den Zehnerübertrag jeder Dezimalstelle zu speichern. Das bedeutet, dass die Rechnung 9+1 einfach zu bewältigen ist, jedoch 9999+1 hohen Kraftaufwand erfordert und vermutlich zu Verklemmungen der Maschine geführt hat.“

„ Es scheint ganz selbstverständlich, dass diese materielle Widrigkeit am Gedanken der Berechenbarkeit von 9999+1 nicht das geringste ändert. Aber machen wir uns klar, dass das daran liegen könnte, dass es eine Recheninstanz gibt, die bei 9999+1 nicht klemmt, nämlich den Mathematiker selbst. Was wäre mit der Idee der Berechenbarkeit, wenn 9999+1 zu rechnen Menschen überfordern würde und eine technische Entität gerade dazu in der Lage wäre? Hätte man es dann mit Ideen zu tun, die nicht gedacht werden können, bevor sie gemacht werden?“

Wichtig ist mir, von vorn herein auf die unterschiedlichen stofflichen Realisierungen von Konzepten zu achten und darauf, dass sich aus unterschiedlichen Realisierungen unterschiedliche Inhaltliche Bestimmungen der Ideen selbst ergeben könnten. Die meisten von uns gehen davon aus, dass eine Idee sich gleich bleibt, ganz unabhängig davon, wie sie stofflich realisiert ist. Die Behauptung einer körperunabhängigen Selbstidentität des Denkens ist z.B. der Kerngedanke des Leib-Seele-Dualismus. Nur wenn Gehalt und physische Realisierung als Getrennte gedacht werden, kann sich überhaupt die Frage stellen, die die heutige Philosophie des Geistes umtreibt, wie sich mentale und physische Zustände zueinander verhalten. Wenn man von einem Leib-Seele-Dualismus ausgeht, kann man auch so etwas denken wie reine, nicht realisierte Ideen, z.B. eine reine Mathematik. Wir werden sehen, dass das maschinelle Lernen, wenn wir es denn so nennen wollen, ein Thema ist, bei dem Ideen durchaus nicht mehr die selben bleiben, je nachdem, wie sie physisch-materiell realisiert werden.

Turing-Vollständigkeit neuronaler Netze

Hier ist allerdings bereits der Ort, um auf etwas hinzuweisen, was grundsätzlich wichtig ist. Perzeptronen/Neuronen sind nicht nur eine Möglichkeit, um zu so etwas wie Entscheidungen zu kommen, sondern sie sind Turing-vollständig. D.h. man kann mit Perzeptronen grundsätzlich universell programmieren. Turing-Vollständigkeit bezeichnet in der Berechenbarkeitstheorie die Eigenschaft einer Programmiersprache etwa von Java oder C++ oder eines anderen logischen Systems, sämtliche Funktionen berechnen zu können, die eine universelle Turingmaschine, also z.B. ein Personalcomputer berechnen kann. Anders ausgedrückt, das System und eine universelle Turingmaschine können sich gegenseitig emulieren.

Der Beweis dafür ist folgender: Man kann Perzeptronen auch dazu verwenden, die elementaren logischen Funktionen wie AND, OR und NAND zu berechnen. NAND ist die logische Funktion, die dann und nur dann falsch wird, wenn beide Prämissen richtig sind. Angenommen, wir haben ein Perzeptron mit zwei Eingängen mit einem Gewicht von jeweils –2 und einen Bias von 3.

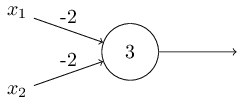
Wenn an x₁ und x₂ jeweils 0 eingegeben wird,erhält man als Entscheidung

(−2) ∗ 0 + (- 2) ∗ 0 + 3 = 3 Eine positive Entscheidung ergibt den Output 1.

Wenn nur an einem von beiden x₁ oder x₂ eine 1 eingegeben wird,erhält man als Entscheidung

(−2) ∗ 1 + (- 2) ∗ 0 + 3 = 1 Diese positive Entscheidung ergibt ebenfalls den Output 1.

Wenn jedoch an beiden, an x₁ und x₂ eine 1 eingegeben wird, erhält man als Entscheidung

(−2) ∗ 1 + (- 2) ∗ -1 + 3 = -1 Diese negative Entscheidung ergibt den Output 0.

Das Netz realisiert also hier ein NAND-Gatter. Man kann also Perzeptronen verwenden, um logische Funktionen zu realisieren. Und man kann damit rechnen. Der Grund ist, dass das NAND-Gatter universell für die Berechnung ist, d.h. man kann alle Berechnungen aus NAND-Gattern aufbauen. Zum Beispiel kann man NAND-Gatter verwenden, um eine Schaltung aufzubauen, die zwei Bits x₁ und x₂ addiert. Dies erfordert die Berechnung der bitweisen Summe x₁⊕x₂ sowie eines Übertragsbits, das auf 1 gesetzt wird, wenn sowohl x₁ als auch x₂ 1 sind, d. H. Das Übertragsbit ist das bitweise Produkt x₁x₂.

Jetzt fragt sich allerdings, was an Neuronalen Netzwerken neu sein soll, wenn Perzeptronen einfach nur eine andere Art von NAND-Gattern realisieren. Woher dann der ganze Zauber mit der KI?

Neu daran ist, dass sich die Gewichte und der Bias sich aufgrund externer Reize automatisch verstellen lassen, denn darauf basiert, was man zu recht oder zu unrecht als die Lernfähigkeit neuronaler Netze bezeichnet. Richtiger müsste es heißen: Neuronale Netze sind Iterationsautomaten.

Aktivierungsfunktionen

Angenommen, wir haben ein Netzwerk von Perzeptronen, mit denen wir lernen möchten, ein Problem zu lösen. Beispielsweise könnten die Eingaben in das Netzwerk die Rohpixeldaten eines gescannten, handgeschriebenen Bildes einer Ziffer sein. Und wir möchten, dass das Netzwerk Gewichte und Bias lernt, damit die Ausgabe des Netzwerks die Ziffer korrekt klassifiziert. Nehmen wir weiter an, wir nehmen eine kleine Änderung eines einzelnen Gewichts im Netzwerk vor, um zu sehen, wie das Lernen funktionieren könnte. Was wir möchten, ist, dass diese kleine Gewichtsänderung nur eine kleine entsprechende Änderung der Ausgabe aus dem Netzwerk verursacht. Das würde per trial and error so etwas wie Lernen ermöglichen.

Wenn es wahr wäre, dass eine kleine Änderung eines Gewichts (oder eines Bias) nur eine kleine Änderung der Ausgabe verursacht, könnten wir diese Tatsache nutzen, um die Gewichte und Bias zu ändern, damit sich das Netzwerk mehr in der von uns gewünschten Weise verhält. Angenommen, das Netzwerk hat das Bild einer Ziffer fälschlicherweise als "8" klassifiziert, wenn es eine "9" sein sollte. Wir könnten herausfinden, wie eine kleine Änderung der Gewichte und Bias vorgenommen werden kann, damit das Netzwerk der Klassifizierung des Bildes als "9" ein Stück näher kommt. Und dann würden wir dies wiederholen und die Gewichte und Bias immer wieder ändern, um eine immer bessere Ausgabe zu erzielen. Das Netzwerk würde 'lernen', dass es sich um eine 9 handelt.

Leider passiert aber oft unvorhersehbar etwas anderes, und kleine Änderungen der Gewichte oder des Bias bewirken große Sprünge der Ergebnisse. Dieser Umschlag kann nämlich dazu führen, dass sich das Verhalten des restlichen Netzwerks auf sehr komplizierte und unvorhersagbare Weise vollständig ändert. Während die "9" jetzt möglicherweise korrekt klassifiziert ist, kann es sein, dass plötzlich andere Ziffern falsch gelesen werden, die zuvor noch korrekt erkannt wurden.

Man muss also versuchen, solche Übersprungereignisse durch den Einsatz bestimmter mathematischer Funktionen, sogenannter Aktivierungsfunktionen zu beheben, mit denen die Entscheidungen der einzelnen Perzeptronen sozusagen geglättet werden, bevor sie als Input an die nächst höhere Schicht weitergegeben werden. Welche speziellen Funktionen für welche Aufgaben geeignete Aktivierungsfunktionen sind, ist Gegenstand intensivster empirischer Forschung und wird permanent weiterentwickelt.¹

Eine gängige nichtlineare Aktivierungsfunktion ist die Sigmoidfunktion.

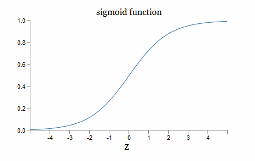
Wie sich einzelne Ziffern erkennen lassen, kann man mit einem dreischichtigen neuronalen Netzwerk verdeutlichen:

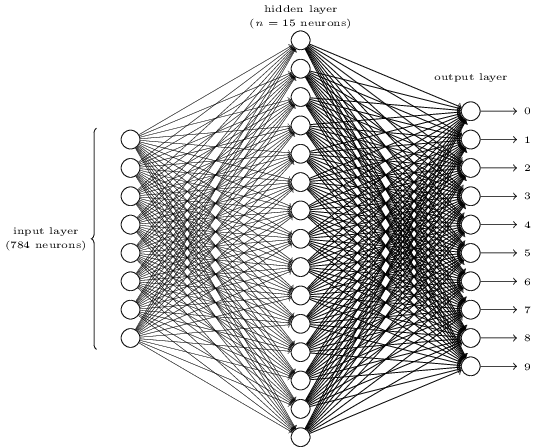
Die Eingabeschicht des Netzwerks enthält Neuronen, die die Werte der Eingabepixel codieren. Die zweite Schicht des Netzwerks ist eine verborgene Schicht. Wir bezeichnen die Anzahl der Neuronen in dieser verborgenen Schicht mit n und wir können mit verschiedenen Werten für n experimentieren. Das obige Beispiel zeigt eine kleine verborgene Schicht, die nur n = 15 Neuronen enthält.

Die Ausgangsschicht des Netzwerks enthält 10 Neuronen. Nach Auswertung aller Layer wird ein bestimmtes Neuron den höchsten Aktivierungswert haben. Wenn dieses Neuron beispielsweise Neuron Nummer 6 ist, wird das Netzwerk vermuten, dass die eingegebene Ziffer eine 5 war. Sofern die Ziffernfolge mit 0 beginnt, ist 5 die 6te Ziffer.

Fehlertoleranz und Redundanz

Bekanntlich kann ein einziger Übertragungsfehler ein komplettes Computerprogramm von tausenden von Code-Zeilen außer Gefecht setzen. Hätte es für dieses Problem keine Lösung gegeben, wäre die heutige Computertechnik unmöglich. Die theoretische Lösung gab der amerikanische Mathematiker Claude Shannon im Juli und Oktober 1948 im Bell System Technical Journal mit seinem Artikel "A Mathematical Theory of Communication". Er demonstrierte dort, wie sich willkürlich genaue Kommunikation auch über die unzuverlässigsten Kommunikationskanäle herstellen lässt. Eine Kanalcodierung kann beliebig verraucht sein, bei genügend häufiger Wiederholung der Information wird es gelingen, sie am Empfänger beliebig korrekt zu lesen. Entscheidend ist die Redundanz. Das gilt außer in dem Fall, in dem die Fehlerrate bei genau 50% liegt, nur dann sind Rauschen und Information ununterscheidbar.

Hat man im Extremfall einen Kanal, der nur in 51 Prozent der Fälle korrekt Informationsbits überträgt, kann man dennoch Nachrichten so übertragen, dass nur jedes millionste Bit oder eine noch geringere Rate fehlerhaft gelesen wird. Wie präzise selbst dann die Übertragung ist, hängt von Redundanz ab. Es ist evident, dass Trainings- wie der Kontrolldaten in der KI die selbe Rolle, wie Shannons Redundanz spielen.

Redundanz ist ein weiterer Hauptaspekt von Ähnlichkeit und der Punkt, an dem Zufall und Regel zusammenkommen.

Voraussetzungslos ist der Begriff der Redundanz allerdings durchaus nicht. Soll er in gewisser Weise Voraussetzung für fehlerfreies Erkennen von Signalen sein und in unserem Fall für das Erkennen von Ähnlichkeiten, dann setzt er natürlich voraus, dass das was redundant gesendet wird, bereits ein Zeichen ist. Redundanz wiederholt etwas, aber es konstituiert es nicht. Solange es im sog. 'schwache' KI geht, ist das wohl kein Problem, aber wenn es um mehr geht, um KI, die ihre eigenen Regeln modifiziert oder um ein Modell für das Erkennen von Ähnlichkeiten im Gehirn des Menschen, wird die Wiederholung selbst zu einem konstituierenden Mechanismus. Natürlich ist das, was das Kind beim Spracherwerb zu hören bekommt, bereits Sprache, aber die Mutter, die spricht und die es im wiederholten Anblick wiedererkennt, ist kein Zeichen. Wenn etwas aus ihr so etwas wie ein Zeichen macht, dann die kognitiven Fähigkeiten des Kindes. Und es sind die selben Fähigkeiten, die sprechen lernen. In sofern erfindet jedes Kind die Sprache neu. Redundanz steht also hier nicht für etwas, das ein Sender solange wiederholt, bis es ein Empfänger verstanden hat, wobei er es eben um so öfter zu wiederholen hat, je undeutlicher er artikuliert, sondern es steht für einen bestimmten Charakterzug eines Schöpfungsakts durch den Empfänger. Es dürfte klar sein, dass das, was wiederholt wird, mehr ist als Input. Denn unter Input versteht man normalerweise etwas, dass in den meisten Fällen bereits bei einmaliger Gabe verarbeitet werden kann, z.B. das Senden eines Werts an ein Programm oder die Eingabe einer Kreditkarte samt gewünschten Geldbetrag und Geheimnummer in einen Geldautomaten oder der Biss in einen Keks. Um Wirkungen zu erzielen braucht man beim Input den Vorgang nicht ständig zu wiederholen. Redundanz dagegen ist eine Form der Wiederholung von Input, von der man in der Regel weder platzt noch pleite geht, sondern die höchstens langweilt, wenn sie die Frische verloren hat, mit der sich ihr das Lernen zuwendet und sich nurmehr die immer gleichen Zeichen wiederholen.²

CAMILLE. „Rasch, Danton, wir haben keine Zeit zu verlieren!“
DANTON er kleidet sich an. ,,Aber die Zeit verliert uns. Das ist sehr langweilig, immer das Hemd zuerst und dann die Hosen drüber zu ziehen und des Abends ins Bett und morgens wieder heraus zu kriechen und einen Fuß immer so vor den anderen zu setzen; da ist gar kein Absehen, wie es anders werden soll. Das ist sehr traurig, und daß Millionen es schon so gemacht haben, und daß Millionen es wieder so machen werden, und daß wir noch obendrein aus zwei Hälften bestehen, die beide das nämliche tun, so daß alles doppelt geschieht - das ist sehr traurig.“
(Büchner, Dantons Tod, 2.Akt)

Redundanz heißt, dass die Wiederholung eine notwendige, wenn auch nicht hinreichende Voraussetzung dafür ist, dass im Wahrnehmenden, es sei ein Mensch oder eine Maschine ein neuer Wert entsteht, oder anders gesagt, dass etwas als ähnlich erkannt wird.

Trainings- und Kontrolldaten

Es reicht also nicht, dass ein elementares Design für ein neuronales Netzwerk definiert ist, es werden jetzt auch Trainingsdatensätze benötigt. Jedem, der es nachprogrammieren möchte, steht heute beispielsweise der MNIST-Datensatz kostenlos zur Verfügung, der Zehntausende gescannter Bilder handgeschriebener Ziffern zusammen mit ihren korrekten Klassifizierungen enthält.

Die MNIST Datensätze stammen von NIST, dem National Institute of Standards and Technology der Vereinigten Staaten. Die MNIST-Daten bestehen aus zwei Teilen. Der erste Teil enthält 60.000 Bilder, die als Trainingsdaten verwendet werden sollen. Bei diesen Bildern handelt es sich um gescannte Handschriftmuster von 250 Personen. Es sind Graustufen-Bilder und sie sind 28 x 28 Pixel groß. Der zweite Teil des MNIST-Datensatzes besteht aus 10.000 Bildern, die als Testdaten verwendet werden sollen. Man verwendet die Testdaten, um zu bewerten, wie gut das neuronale Netzwerk gelernt hat, Ziffern zu erkennen. Auch dies sind 28 x 28 Graustufenbilder.

Jede Trainingseingabe x wird als ein 28 × 28 = 784-dimensionaler Vektor betrachtet. Jeder Eintrag im Vektor repräsentiert den Grauwert für ein einzelnes Pixel im Bild. Wir bezeichnen die entsprechende gewünschte Ausgabe mit y = y(x), wobei y ein 10-dimensionaler Vektor ist. Wenn beispielsweise ein bestimmtes Trainingsbild x eine 6 darstellen soll, ist y (x) = (0,0,0,0,0,0,1,0,0,0) T die gewünschte Ausgabe aus dem Netzwerk. Die 1 steht an siebter Stelle und nicht an sechster, weil wie gesagt die Reihe mit Null und nicht mit Eins beginnt.

Kostenfunktion

Die sukzessive Verbesserung der Erkennungsergebnisse ist ein iterativer Vorgang. Wie funktioniert dabei das Anpassen der Gewichte mathematisch? Hier kommt die so genannte Kostenfunktion ins Spiel. Neuronale Netze lernen, indem sie iterativ die Modellprognosen mit den tatsächlich beobachteten Daten vergleichen und die Gewichtungsfaktoren im Netz so anpassen, dass in jeder Iteration der Fehler zwischen Modellprognose und Ist-Daten kleiner wird. Aber wie machen sie das?

Zur Quantifizierung des Modellfehlers wird dann jeweils eine Kostenfunktion errechnet. Diese hat normalerweise zwei Funktionsargumente, nämlich den Output des Modells (Ŷ), sowie die tatsächlich beobachteten Daten (Y). Eine in neuronalen Netzen häufig verwendete Kostenfunktion ist der mittlere quadratische Fehler (Mean Squared Error, MSE)...

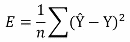
...wobei Ŷ für die Vorhersage, also den geschätzten Wert steht und Y für den tatsächlich gemessenen Wert. Der Vorteil des quadratischen Fehlers (neben vielen anderen denkbaren Kostenfunktionen, denn auch die Kostenfunktion muss empirisch bewertet werden) ist, dass sich ein kleiner Fehler kaum auswirkt, ein großer Fehler durch die Quadrierung jedoch enorm.

Der MSE errechnet zunächst für jeden Datenpunkt die quadratische Differenz zwischen y_i und y und bildet dann den Mittelwert. Ein hoher MSE reflektiert somit eine schlechte Anpassung des Modells an die vorliegenden Daten. Ziel des Modelltrainings soll es sein, die Kostenfunktion durch Anpassung der Modellparameter (Gewichtungen) zu minimieren.

Doch woher weiß das neuronale Netz, welche Gewichte angepasst werden müssen und in welche Richtung? Faktisch hängt die Kostenfunktion immer von sämtlichen Parametern im neuronalen Netz ab. Verändert man auch nur ein Gewicht minimal, hat dies eine unmittelbare Auswirkung auf alle folgenden Neuronen und damit den Ausgang des Netzes und daher auch auf die Kostenfunktion.

In der Mathematik lassen sich die Stärke und Richtung der Veränderung der Kostenfunktion durch Veränderung eines einzelnen Parameters im Netzwerk durch die Berechnung der partiellen Ableitung der Kostenfunktion nach dem entsprechenden Gewichtungsparameter ermitteln.

Da die Kostenfunktion sozusagen hierarchisch von den einzelnen Gewichtungsfaktoren im Netz abhängt, muss man jetzt mathematisch nur noch jeweils die Ableitungen bilden, um zu bestimmen, wie die Gewichte zu aktualisieren sind.

Anmerkungen: